在机器学习中,KL散度,JS散度,交叉熵这三个指标都是比较不好区分差异的,小编在看论文《Detecting Regions of Maximal Divergence for Spatio-Temporal Anomaly Detection》时,看到文中提到了这三种方法来比较时间序列中不同区域概率分布的差异。特意分享出来给各位小伙伴们加深理解。
KL散度、JS散度和交叉熵
三者都是用来衡量两个概率分布之间的差异性的指标。不同之处在于它们的数学表达。
对于概率分布P(x)和Q(x)
1)KL散度(Kullback–Leibler divergence)
又称KL距离,相对熵。
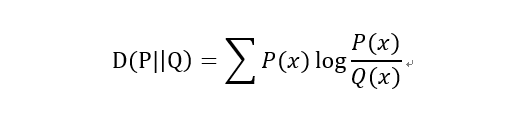
当P(x)和Q(x)的相似度越高,KL散度越小。
KL散度主要有两个性质:
(1)不对称性
尽管KL散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即D(P||Q)!=D(Q||P)。
(2)非负性
相对熵的值是非负值,即D(P||Q)>0。
2)JS散度(Jensen-Shannon divergence)
JS散度也称JS距离,是KL散度的一种变形。
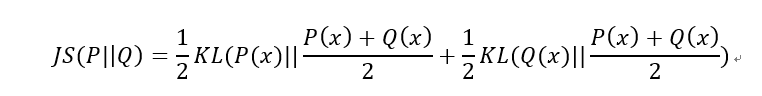
但是不同于KL主要又两方面:
(1)值域范围
JS散度的值域范围是[0,1],相同则是0,相反为1。相较于KL,对相似度的判别更确切了。
(2)对称性
即 JS(P||Q)=JS(Q||P),从数学表达式中就可以看出。
3)交叉熵(Cross Entropy)
在神经网络中,交叉熵可以作为损失函数,因为它可以衡量P和Q的相似性。
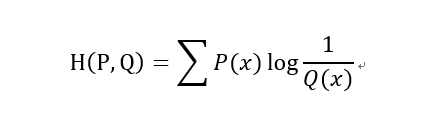
交叉熵和相对熵的关系:
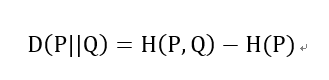
以上都是基于离散分布的概率,如果是连续的数据,则需要对数据进行Probability Density Estimate来确定数据的概率分布,就不是求和而是通过求积分的形式进行计算了。
补充:信息熵、交叉熵与KL散度
信息量
在信息论与编码中,信息量,也叫自信息(self-information),是指一个事件所能够带来信息的多少。一般地,这个事件发生的概率越小,其带来的信息量越大。
从编码的角度来看,这个事件发生的概率越大,其编码长度越小,这个事件发生的概率越小,其编码长度就越大。但是编码长度小也是代价的,比如字母'a'用数字‘0'来表示时,为了避免歧义,就不能有其他任何以‘0'开头的编码了。
因此,信息量定义如下:

信息熵
信息熵是指一个概率分布p的平均信息量,代表着随机变量或系统的不确定性,熵越大,随机变量或系统的不确定性就越大。从编码的角度来看,信息熵是表示一个概率分布p需要的平均编码长度,其可表示为:
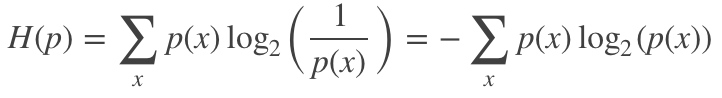
交叉熵
交叉熵是指在给定真实分布q情况下,采用一个猜测的分布p对其进行编码的平均编码长度(或用猜测的分布来编码真实分布得到的信息量)。
交叉熵可以用来衡量真实数据分布于当前分布的相似性,当前分布与真实分布相等时(q=p),交叉熵达到最小值。
其可定义为:
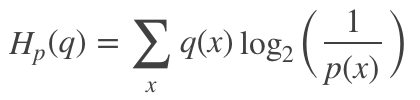
因此,在很多机器学习算法中都使用交叉熵作为损失函数,交叉熵越小,当前分布与真实分布越接近。此外,相比于均方误差,交叉熵具有以下两个优点:
在LR中,如果用均方误差损失函数,它是一个非凸函数,而使用交叉熵损失函数,它是一个凸函数;
在LR中使用sigmoid激活函数,如果使用均方误差损失函数,在对其求残差时,其表达式与激活函数的导数有关,而sigmoid(如下图所示)的导数在输入值超出[-5,5]范围后将非常小,这会带来梯度消失问题,而使用交叉熵损失函数则能避免这个问题。
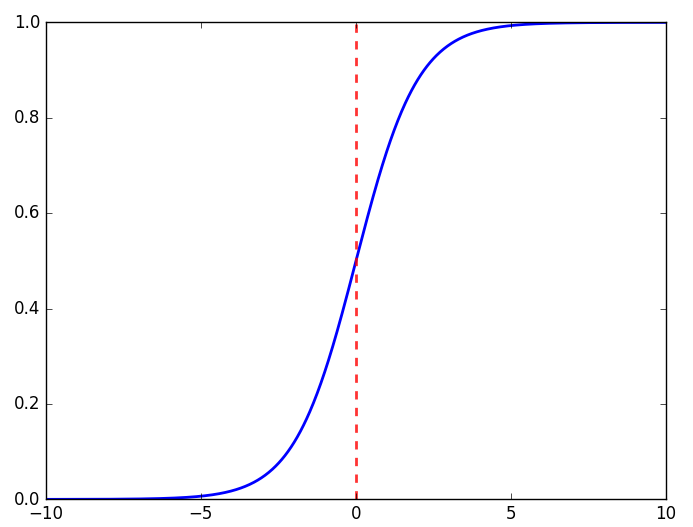
KL散度
KL散度又称相对熵,是衡量两个分布之间的差异性。从编码的角度来看,KL散度可表示为采用猜测分布p得到的平均编码长度与采用真实分布q得到的平均编码长度多出的bit数,其数学表达式可定义为:

一般地,两个分布越接近,其KL散度越小,最小为0.它具有两个特性:
非负性,即KL散度最小值为0,其详细证明可见[1] ;
非对称性,即Dq(p)不等于Dp(q) ; KL散度与交叉熵之间的关系
在这里,再次盗用[1]的图来形象地表达这两者之间的关系:
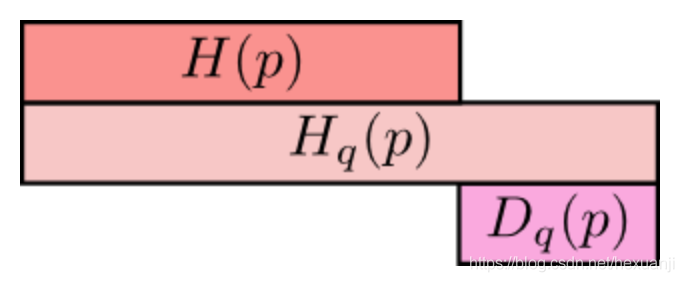
最上方cH(p)为信息熵,表示分布p的平均编码长度/信息量;
中间的Hq(p)表示用分布q表编码分布p所含的信息量或编码长度,简称为交叉熵,其中Hq(p)>=H(p)
;最小方的Dq(p)表示的是q对p的KL距离,衡量了分布q和分布p之间的差异性,其中Dq(p)>=0;
从上图可知,Hq(p) = H(p) + Dq(p)。
小结
以上就是关于KL散度,JS散度,交叉熵的对比,希望能给大家一个参考,也希望大家多多支持W3Cschool。

 免费AI编程助手
免费AI编程助手



