拉格朗日插值法是一种用来进行曲线拟合和回归的一种方法,但其计算比较不方便,后来牛顿提出了牛顿插值法,这种方法运算起来比拉格朗日法更加简单。今天我们就来介绍牛顿插值法的相关内容,也顺便介绍一下牛顿插值法的C++与python实现。
一、牛顿多项式
拉格朗日多项式的公式不具备递推性,每个多项式需要单独构造。但很多时候我们需要从若干个逼近多项式选择一个。这个时候我们就需要一个具有递推关系的方法来构造——牛顿多项式
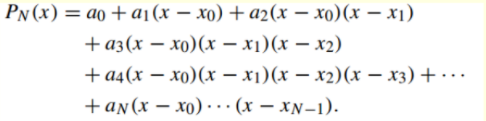
这里的的a0,a1…等可以通过逐一带入点的值来求得。但是当项数多起来时,会发现式子变得很大,这个时候我们便要引入差商的概念(利用差分思想)具体见式子能更好理解


这里在编程实现中我们可以推出相应的差商推导方程
d(k,0)=y(k)
d(k,j)=(d(k,j-1)-d(k-1,j-1)) / (x(k)-x(k-j))
二、例题
【问题描述】考虑[0,3]内的函数y=f(x)=cos(x)。利用多个(最多为6个)节点构造牛顿插值多项式。
【输入形式】在屏幕上依次输入在区间[0,3]内的一个值x*,构造插值多项式后求其P(x*)值,和多个节点的x坐标。
【输出形式】输出牛顿插值多项式系数向量,差商矩阵,P(x*)值(保留6位有效数字),和与真实值的绝对误差(使用科学计数法,保留小数点后6位有数字)。
【样例1输入】
0.8
0 0.5 1
【样例1输出】
-0.429726
-0.0299721
1
1 0 0
0.877583 -0.244835 0
0.540302 -0.674561 -0.429726
0.700998
4.291237e-03
【样例1说明】
输入:x为0.8,3个节点为(k, cos(k)),其中k = 0, 0.5, 1。
输出:
牛顿插值多项式系数向量,表示P2(x)=-0.429726x^2 - 0.0299721x + 1;
3行3列的差商矩阵;
当x为0.8时,P2(0.8)值为0.700998
与真实值的绝对误差为:4.291237*10^(-3)
【评分标准】根据输入得到的输出准确
三、ACcode:
C++(后面还有python代码)
/*
* @Author: csc
* @Date: 2021-04-30 08:52:45
* @LastEditTime: 2021-04-30 11:57:46
* @LastEditors: Please set LastEditors
* @Description: In User Settings Edit
* @FilePath: code_formalcoursecal
ewton_quo.cpp
*/
#include <bits/stdc++.h>
#define pr printf
#define sc scanf
#define for0(i, n) for (i = 0; i < n; i++)
#define for1n(i, n) for (i = 1; i <= n; i++)
#define forab(i, a, b) for (i = a; i <= b; i++)
#define forba(i, a, b) for (i = b; i >= a; i--)
#define pb push_back
#define eb emplace_back
#define fi first
#define se second
#define int long long
#define pii pair<int, int>
#define vi vector<int>
#define vii vector<vector<int>>
#define vt3 vector<tuple<int, int, int>>
#define mem(ara, n) memset(ara, n, sizeof(ara))
#define memb(ara) memset(ara, false, sizeof(ara))
#define all(x) (x).begin(), (x).end()
#define sq(x) ((x) * (x))
#define sz(x) x.size()
const int N = 2e5 + 100;
const int mod = 1e9 + 7;
namespace often
{
inline void input(int &res)
{
char c = getchar();
res = 0;
int f = 1;
while (!isdigit(c))
{
f ^= c == '-';
c = getchar();
}
while (isdigit(c))
{
res = (res << 3) + (res << 1) + (c ^ 48);
c = getchar();
}
res = f ? res : -res;
}
inline int qpow(int a, int b)
{
int ans = 1, base = a;
while (b)
{
if (b & 1)
ans = (ans * base % mod + mod) % mod;
base = (base * base % mod + mod) % mod;
b >>= 1;
}
return ans;
}
int fact(int n)
{
int res = 1;
for (int i = 1; i <= n; i++)
res = res * 1ll * i % mod;
return res;
}
int C(int n, int k)
{
return fact(n) * 1ll * qpow(fact(k), mod - 2) % mod * 1ll * qpow(fact(n - k), mod - 2) % mod;
}
int exgcd(int a, int b, int &x, int &y)
{
if (b == 0)
{
x = 1, y = 0;
return a;
}
int res = exgcd(b, a % b, x, y);
int t = y;
y = x - (a / b) * y;
x = t;
return res;
}
int invmod(int a, int mod)
{
int x, y;
exgcd(a, mod, x, y);
x %= mod;
if (x < 0)
x += mod;
return x;
}
}
using namespace often;
using namespace std;
int n;
signed main()
{
auto polymul = [&](vector<double> &v, double er) {
v.emplace_back(0);
vector<double> _ = v;
int m = sz(v);
for (int i = 1; i < m; i++)
v[i] += er * _[i - 1];
};
auto polyval = [&](vector<double> const &c, double const &_x) -> double {
double res = 0.0;
int m = sz(c);
for (int ii = 0; ii < m; ii++)
res += c[ii] * pow(_x, (double)(m - ii - 1));
return res;
};
int __ = 1;
//input(_);
while (__--)
{
double _x, temp;
cin >> _x;
vector<double> x, y;
while (cin >> temp)
x.emplace_back(temp), y.emplace_back(cos(temp));
n = x.size();
vector<vector<double>> a(n, vector<double>(n));
int i, j;
for0(i, n) a[i][0] = y[i];
forab(j, 1, n - 1) forab(i, j, n - 1) a[i][j] = (a[i][j - 1] - a[i - 1][j - 1]) / (x[i] - x[i - j]);
vector<double> v;
v.emplace_back(a[n - 1][n - 1]);
forba(i, 0, n - 2)
{
polymul(v, -x[i]);
int l = sz(v);
v[l - 1] += a[i][i];
}
for0(i, n)
pr("%g
", v[i]);
for0(i, n)
{
for0(j, n)
pr("%g ", a[i][j]);
puts("");
}
double _y = polyval(v, _x);
pr("%g
", _y);
pr("%.6e",fabs(_y-cos(_x)));
}
return 0;
}
python代码
'''
Author: csc
Date: 2021-04-29 23:00:57
LastEditTime: 2021-04-30 09:58:07
LastEditors: Please set LastEditors
Description: In User Settings Edit
FilePath: code_py
ewton_.py
'''
import numpy as np
def difference_quotient(x, y):
n = len(x)
a = np.zeros([n, n], dtype=float)
for i in range(n):
a[i][0] = y[i]
for j in range(1, n):
for i in range(j, n):
a[i][j] = (a[i][j-1]-a[i-1][j-1])/(x[i]-x[i-j])
return a
def newton(x, y, _x):
a = difference_quotient(x, y)
n = len(x)
s = a[n-1][n-1]
j = n-2
while j >= 0:
s = np.polyadd(np.polymul(s, np.poly1d(
[x[j]], True)), np.poly1d([a[j][j]]))
j -= 1
for i in range(n):
print('%g' % s[n-1-i])
for i in range(n):
for j in range(n):
print('%g' % a[i][j], end=' ')
print()
_y = np.polyval(s, _x)
print('%g' % _y)
# re_err
real_y = np.cos(_x)
err = abs(_y-real_y)
print('%.6e' % err)
def main():
_x = float(input())
x = list(map(float, input().split()))
y = np.cos(x)
newton(x, y, _x)
if __name__ == '__main__':
main()
到此这篇Python牛顿插值法的文章就介绍到这了,更多Python算法实现内容请搜索W3Cschool以前的文章或继续浏览下面的相关文章。

 免费AI编程助手
免费AI编程助手



